Tipos de conjuntos matemáticos

Daniel Machado · Actualizado el 10/06/2025

Existen diferentes clases de conjuntos en la teoría de conjuntos, varios de estos los recopilamos en la siguiente tabla:

Nombre	Descripción	Ejemplos
Conjunto finito	Un conjunto finito es aquel que tiene un número limitado de elementos.	A = {a, e, i, o, u} B = {x \| x es una vocal}
Conjunto infinito	Un conjunto infinito es aquel que tiene un número ilimitado de elementos.	N = {1, 2, 3, ...} (el conjunto de los números naturales). P = {x \| x es par} (el conjunto de los números enteros pares).
Conjunto vacío	El conjunto vacío, representado por { } o Ø, es aquel que no tiene elementos.	El conjunto de planetas que orbitan alrededor de la luna es Ø El conjunto de soluciones de la ecuación x ⋅ 0 = 4 es vacío: Ø = {x \| x ⋅ 0 = 4}
Conjunto unitario	Un conjunto unitario es aquel que contiene un solo elemento.	A = {z} es unitario. El conjunto de soluciones de la ecuación 2 ⋅ x = 4 es unitario: {x \| 2⋅x = 4} = {2}
Conjunto universal	El conjunto universal es aquel que contiene todos los elementos relevantes para un determinado contexto.	Al trabajar con números naturales, el conjunto universal es el de todos los números naturales: N. Al trabajar con triángulos, el conjunto universal es el de todos los triángulos.
Conjunto complementario	El complemento de un conjunto A, simbolizado como A', es el conjunto de todos los elementos que están en el conjunto universal pero no están en A.	El complemento del conjunto de los números enteros impares es el conjunto de enteros pares. El complemento del conjunto de los triángulos equiláteros es el conjunto de los triángulos que no son equiláteros (isósceles y escalenos).
Conjunto de partes	El conjunto de partes o conjunto potencia de un conjunto es el conjunto que contiene todos los subconjuntos posibles de ese conjunto original.	El conjunto de partes de A = {a, b} es P(A) = {Ø, {a}, {b}, {a, b}}. El conjunto de partes de Ø es P(Ø) = {Ø}.
Conjuntos numéricos	Los conjuntos numéricos son conjuntos que contienen números con ciertas características comunes.	Números naturales (N) Números enteros (Z) Números racionales (Q) Números irracionales (I) Números reales (R) Números complejos (C)
Subconjunto	Un conjunto A es un subconjunto de otro conjunto B si todos los elementos de A también están en B.	El conjunto A = {perro, gato} es subconjunto de B = {perro, gato, pájaro}. El conjunto de los números naturales N es un subconjunto de los números enteros Z.
Subconjunto propio	Un conjunto A es subconjunto propio de B si todos los elementos a A también están en B pero A ≠ B.	A = {1, 2} es un subconjunto propio de B = {1, 2, 3}. El conjunto de los enteros pares es un subconjunto propio de los números enteros.
Conjuntos equivalentes	Dos conjuntos son equipotentes o equivalentes si tienen la misma cantidad de elementos (mismo cardinal).	Los conjuntos A = {a, b, c} y B = {7, 8, 9} son equipotentes por tener la misma cantidad de elementos. El conjunto de letras de la palabra "gato" y el conjunto de números enteros del 1 al 4 son equivalentes porque ambos tienen cuatro elementos.
Conjuntos iguales	Dos conjuntos son iguales si tienen los mismos elementos, sin importar el orden.	El conjunto A = {a, b, c} es igual al B = {c, b, a}. El conjunto {1, -1} es igual al conjunto {x \| x² = 1}
Conjuntos disjuntos	Dos conjuntos son disjuntos si no comparten ningún elemento en común.	Los conjuntos A = {1, 2} y B = {3, 4} son disjuntos porque no comparten ningún elemento. El conjunto de los números reales positivos y de los reales negativos son disjuntos, porque no existe ningún número que sea positivo y negativo a la vez.

Bibliografía

Corral de Franco, Y. y Manzanares, L. (2018). Nociones Elementales de lógica matemática y teoría de conjuntos. Caracas. Fondo editorial OPSU.
Gentile, E. (1984). Notas de Álgebra I. Editorial Universitaria de Buenos Aires.
Grimaldi, R. (1997). Matemáticas discreta y combinatoria (3ra edición). Addison-Wesley Iberoamericana.
Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.

Profesor de matemáticas y administrador de Axioset, donde comparte contenido acerca de lógica matemática y teoría de conjuntos.

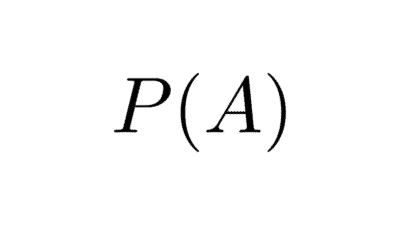
Otros artículos que pueden interesarte

Deja una respuesta Cancelar la respuesta

Subir