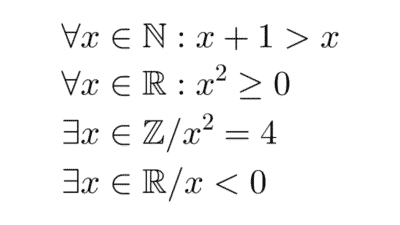
Leyes lógicas

Daniel Machado · Actualizado el 10/06/2025

Una ley lógica o tautología es una proposición compuesta que siempre es verdadera independientemente del valor de verdad de las proposiciones componentes. Para demostrar una ley lógica es suficiente confeccionar su tabla de verdad.

Índice

Leyes lógicas básicas

Las leyes básicas de la lógica son aquellas con las que solemos trabajar habitualmente. Las veremos todas a continuación.

Nombre	Simbología	Descripción
Involución	¬(¬p) ≡ p	La negación de la negación de una proposición es equivalente a la proposición
Ley de De Morgan de negación de la conjunción	¬(p ∧ q) ≡ ¬p ∨ ¬q	La negación de la conjunción es equivalente a la disyunción de las negaciones
Ley de De Morgan de negación de la disyunción	¬(p ∨ q) ≡ ¬p ∧ ¬q	La negación de la disyunción es equivalente a la conjunción de las negaciones
Conmutatividad	p ∨ q ≡ q ∨ p p ∧ q ≡ q ∧ p	Podemos permutar el orden de escritura de las proposiciones de una conjunción o una disyunción
Asociatividad	p ∨ (q ∨ r) ≡ (p ∨ q) ∨ r p ∧ (q ∧ r) ≡ (p ∧ q) ∧ r	Está permitido asociar proposiciones en una cadena de conjunciones o de disyunciones
Distributividad	(p ∨ q) ∧ r ≡ (p ∧ r) ∨ (q ∧ r) (p ∧ q) ∨ r ≡ (p ∨ r) ∧ (q ∨ r)	La conjunción es distributiva respecto a la disyunción y viceversa
Ley del tercero excluido	p ∨ ¬p	En lógica, una proposición puede ser verdadera o falsa, sin posibilidad de una tercera opción
Ley de la no contradicción	¬ (p ∧ ¬p)	No puede ocurrir que una proposición sea verdadera y falsa al mismo tiempo
Idempotencia	p ∧ p ≡ p p ∨ p ≡ p	La conjunción o disyunción de una proposición consigo misma es equivalente a la misma proposición
Leyes de identidad	p → p p ↔ p	Una proposición es lógicamente equivalente a sí misma
Leyes de transposición	(p → q) ≡ (¬q → ¬p) (p ↔ q) ≡ (¬q ↔ ¬p)	La implicación lógica puede expresarse en forma contrarrecíproca y el bicondicional de dos proposiciones es equivalente al bicondicional de las negaciones
Definición de condicional	p → q ≡ ¬p ∨ q	El condicional es equivalente a la disyunción entre la negación del antecedente y el consecuente
Definición de bicondicional o equivalencia	(p ↔ q) ≡ [(p → q) ∧ (q → p)] (p ↔ q) ≡ [(p ∧ q) ∨ (¬p ∧ ¬q)]	El bicondicional es equivalente a la conjunción de dos condicionales: uno de ida y otro de vuelta
Negación del condicional	¬(p → q) ≡ p ∧ ¬q	La negación de un condicional es equivalente a la conjunción del antecedente y la negación del consecuente
Negación del bicondicional	¬(p ↔ q) ≡ (p ∧ ¬q) ∨ (¬p ∧ q)	Negar una equivalencia es lo mismo que afirmar que una proposición es verdadera y la otra falsa, o viceversa
Leyes de absorción	p ∨ (p ∧ q) ≡ p p ∧ (p ∨ q) ≡ p	La disyunción de una proposición con una conjunción donde ella misma aparece es equivalente a la proposición original, lo mismo ocurre si se intercambian los símbolos
Ley de permutación	[p → (q → r)] ≡ [q → (p → r)]	El orden de los antecedentes en una implicación encadenada puede invertirse sin alterar su valor lógico.
Leyes de expansión	(p → q) ≡ [(p ∨ q) ↔ q] (p → q) ≡ [(p ∧ q) ↔ p]	Un condicional puede expresarse como un bicondicional entre la conjunción (o disyunción) de sus componentes y el consecuente (o el antecedente)

Reglas de inferencia

Las reglas de inferencia son patrones que permiten deducir una nueva proposición válida a partir de una o más proposiciones premisas que se consideran verdaderas.

Nombre	Simbología
Modus Ponens	[(p → q) ∧ p] → q
Modus Tollens	[(p → q) ∧ ¬q] → ¬p
Silogismo	(p → q) → [(q → r) → ( p → r)]
Silogismo disyuntivo	[(p ∨ q) ∧ ¬p] → q [(p ∨ q) ∧ ¬q] → p
Transitividad o silogismo hipotético	[(p → q) ∧ (q → r)] → (p → r) [(p ↔ q) ∧ (q ↔ r)] → (p ↔ r)
Simplificación	p ∧ q → p p ∧ q → q
Adición	p → p ∨ q q → p ∨ q
Dilema constructivo	[( p ∨ q) ∧ ( p → r) ∧ (q → r)] → r
Segunda ley del dilema constructivo	[(p → q) ∧ (r → s) ∧ (p ∨ r)] → (q ∨ s)
Dilema destructivo	[(p → q) ∧ (r → s) ∧ (¬q ∨ ¬s) ] → (¬p ∨ ¬r)
Ley de casos	[(p → q) ∧ (¬p → ¬q)] → q
Exportación	[(p ∧ q) → r] ≡ [p → (q ∧ r)]

Bibliografía

Acevedo González, G. (2011). Lógica Matemática. Universidad Nacional Abierta y a Distancia (UNAD).
Castillo P, E. y Pinta, M. (2015). Lógica Matemática I: Proposiciones y Leyes de Inferencia (2da edición). Universidad Técnica de Machala.
Copi, I. y Cohen, C. (2013). Introducción a la Lógica (2da edición). Limusa.
Garrido, M. (1974). Lógica simbólica (4ta edición). Tecnos.
Gentile, E. (1984). Notas de Álgebra I. Editorial Universitaria de Buenos Aires.
Moreno, A. (1969). Lógica matemática: antecedentes y fundamentos. Editorial Universitaria de Buenos Aires.
Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.