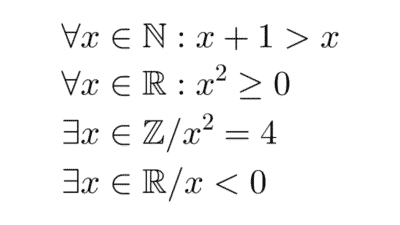
Símbolos lógicos
Los símbolos lógicos son caracteres utilizados en lógica matemática para representar proposiciones, conectores, cuantificadores y relaciones de manera formal y precisa. Estos símbolos permiten estructurar argumentos, demostrar teoremas y analizar la validez de razonamientos.
Para representar proposiciones se usan las letras p, q, r, s...
| Símbolo | Nombre | Significado | Ejemplo |
|---|---|---|---|
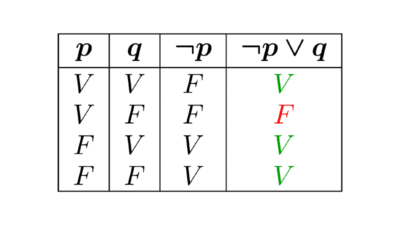
| ¬ | Negación | "no" | ¬p ("no p") |
| ∧ | Conjunción | "y" | p ∧ q ("p y q") |
| ∨ | Disyunción inclusiva | "o" (pueden ser ambos) | p ∨ q ("p o q, o ambos") |
| ⊻ | Disyunción exclusiva | "o" (pero no ambos) | p ⊻ q ("p o q, pero no ambos") |
| → | Condicional (Implicación) | "si… entonces" | p → q ("si p, entonces q") |
| ↔ | Bicondicional (Doble implicación) | "si y sólo si" | p ↔ q ("p si y sólo si q") |
| ∀ | Cuantificador universal | "para todo" | ∀x ∈ ℕ : x ≥ 0 ("todo número natural es no negativo") |
| ∃ | Cuantificador existencial | "existe al menos un" | ∃x ∈ ℝ / x2 = 2 ("existe un número real cuyo cuadrado es 2") |
| ∃! | Cuantificador de existencia única | "existe solo un" | ∃! x ∈ ℤ / 1 + x = 2 ("existe solo un entero que sumado a 1 da resultado 2") |
| ∄ | Cuantificador de negación existencial | "no existe" | ∄ x ∈ ℚ / x2 = 2 ("no existe ningún racional cuyo cuadrado sea 2") |
Deja una respuesta

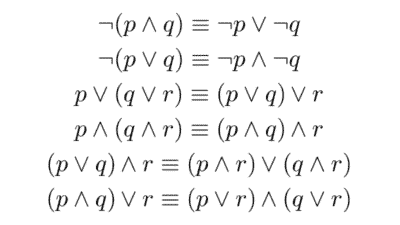


Otros artículos que pueden interesarte