Operaciones entre conjuntos
Existen cinco operaciones entre conjuntos: unión, intersección, diferencia, diferencia simétrica y complementación. A continuación veremos sus definiciones con ejercicios resueltos de cada una.
Índice
Unión de conjuntos
La unión de A y B es el conjunto formado por los elementos de A o de B o de ambos conjuntos. Se lo simboliza como A ∪ B y se lee "A unión B".
A ∪ B = {x | x ∈ A ∨ x ∈ B}
Para calcular la unión de dos conjuntos debemos juntar los elementos de ambos en un solo conjunto. Por ejemplo:
Si A = {1, 4, 6} y B = {7, 6, 9, 2}, entonces:
A ∪ B = {1, 2, 4, 6, 7, 9}
Nótese que, si hay elementos repetidos, en la unión solo se escriben una vez.
Intersección de conjuntos
La intersección de A y B es el conjunto formado por los elementos que pertenecen a ambos simultáneamente. Se lo simboliza como A ∩ B y se lee "A intersección B".
A ∩ B = {x | x ∈ A ∧ x ∈ B}
Para calcular la intersección de dos conjuntos debemos fijarnos en los elementos comunes a ellos. Por ejemplo:
Si A = {1, 4, 6, 2} y B = {7, 6, 9, 2}, entonces:
A ∩ B = {2, 6}
Si ocurre que los conjuntos no tienen elementos en común, la unión es igual al conjunto vacío, en tal caso se dice que los conjuntos son disjuntos. Por ejemplo, si C = {2, 5} y D = {3, 7} entonces C ∩ D = ϕ.
Diferencia de conjuntos
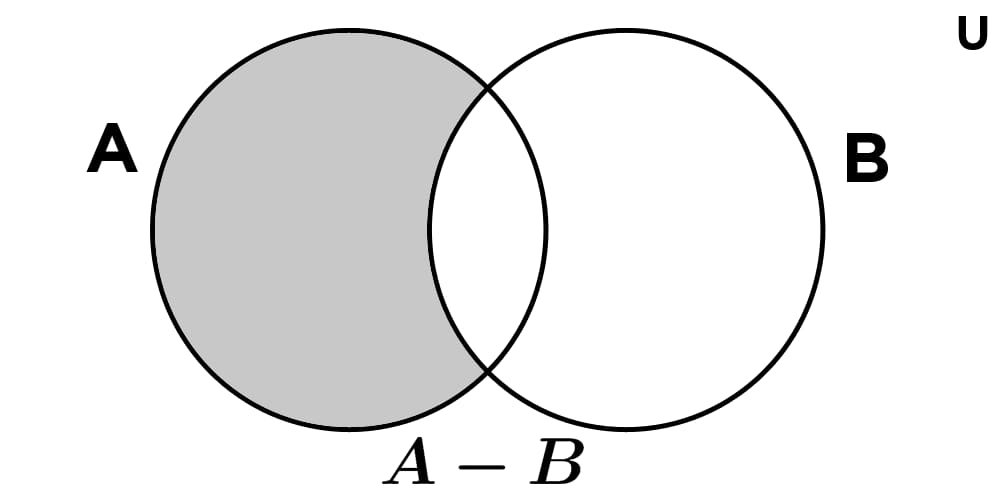
Diferencia entre dos conjuntos A y B es el conjunto formado por los elementos del primero que no pertenecen al segundo. Se simboliza como A - B y se lee "A menos B".
A - B = {x | x ∈ A ∧ x ∉ B}
Para calcular la diferencia entre dos conjuntos debemos tomar los elementos del primer conjunto excluyendo aquellos que comparte con el segundo. Por ejemplo:S
Si A = {a, b, c, d} y B = {a, k, m}, entonces:
A - B = {b, c, d}
Diferencia simétrica de conjuntos
La diferencia simétrica de dos conjuntos A y B se denota por A Δ B, y está formada por todos los elementos que pertenecen a uno de los dos conjuntos, pero no a ambos. En otros términos, es la unión de A - B con B - A:
A Δ B = (A - B) ∪ (B - A)
Para calcular la diferencia simétrica de dos conjuntos primero debemos calcular sus diferencias y luego unirlas en un mismo conjunto. Por ejemplo:
Sean A = {1, 4, 5} y B = {0, 4, 9}, calculamos:
A - B = {1, 5}
B - A = {0, 9}
Con esto obtenemos:
A Δ B = {1, 5, 0, 9}
Complementación de conjuntos
Llamamos conjunto universal, simbolizado como U, a aquel que contiene a todos los elementos relacionados con aquello que estamos trabajando. Por ejemplo, si trabajamos con conjuntos de letras como A = {c, d, e}, el conjunto universal sería el que contiene todas las letras del alfabeto. Si trabajamos con conjuntos de números, se suele considerar como universal al conjunto de los números reales, salvo que se indique lo contrario. En vista de esto, se define lo siguiente:
El complemento de un conjunto A es el conjunto cuyos elementos pertenecen al universal pero no pertenecen a A. Se lo simboliza como CA, A', Ā o Ac y se lee "complemento de A".
Ac = {x | x ∈ U ∧ x ∉ A}
Podemos deducir rápidamente que Ac = U - A
Para calcular el complemento de un conjunto A, hay que primero conocer el conjunto universal U, luego excluir de él a todos los elementos de A. Por ejemplo:
Sea el universal U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} y el conjunto A = {1, 2, 3, 4}, el complemento de A es:
Ac = {5, 6, 7, 8, 9, 10}
Propiedades de las operaciones
Veremos a continuación las propiedades más importantes de la unión, la intersección y el complemento. Si A, B y C son tres conjuntos, U es el universal y ϕ el conjunto vacío, entonces se cumplen las siguientes leyes:
| Propiedad | Simbología |
|---|---|
| Idempotencia | A ∪ A = A A ∩ A = A |
| Asociatividad | (A ∪ B) ∪ C = A ∪ (B ∪ C) (A ∩ B) ∩ C = A ∩ (B ∩ C) |
| Conmutatividad | A ∪ B = B ∪ A A ∩ B = B ∩ A |
| Distributividad | A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) |
| Elementos neutros | A ∪ ϕ = A A ∩ U = A |
| Elementos absorbentes | A ∪ U = U A ∩ ϕ = ϕ |
| Leyes del complemento | (Ac)c = A A ∪ Ac = U Ac = ϕ A ∩ Ac = ϕ ϕc = U |
| Leyes de De Morgan | (A ∪ B)c = Ac ∩ Bc (A ∩ B)c = Ac ∪ Bc |
Ejercicios para practicar
Ejercicio: Dados los siguientes conjuntos:
U = { x | x es un número entero entre -3 y 10 inclusive }
A = {1, 3, 5, 7, 9}
B = {-3, -2, -1, 0, 1, 2, 3}
Obtener:
- A ∪ B
- A ∩ B
- A - B
- B - A
- A Δ B
- Ac
- Bc
Soluciones:
- A ∪ B = {-3, -2, -1, 0, 1, 2, 3, 5, 7, 9}
- A ∩ B = {1, 3}
- A - B = {5, 7, 9}
- B - A = {-3, -2, -1, 0, 2}
- A Δ B = {-3, -2, -1, 0, 2, 5, 7, 9}
- Ac = {-3, -2, -1, 0, 2, 4, 6, 8, 10}
- Bc = {4, 5, 6, 7, 8, 9, 10}
Bibliografía
- Corral de Franco, Y. y Manzanares, L. (2018). Nociones Elementales de lógica matemática y teoría de conjuntos. Caracas. Fondo editorial OPSU.
- Gentile, E. (1984). Notas de Álgebra I. Editorial Universitaria de Buenos Aires.
- Grimaldi, R. (1997). Matemáticas discreta y combinatoria (3ra edición). Addison-Wesley Iberoamericana.
- Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.
Deja una respuesta

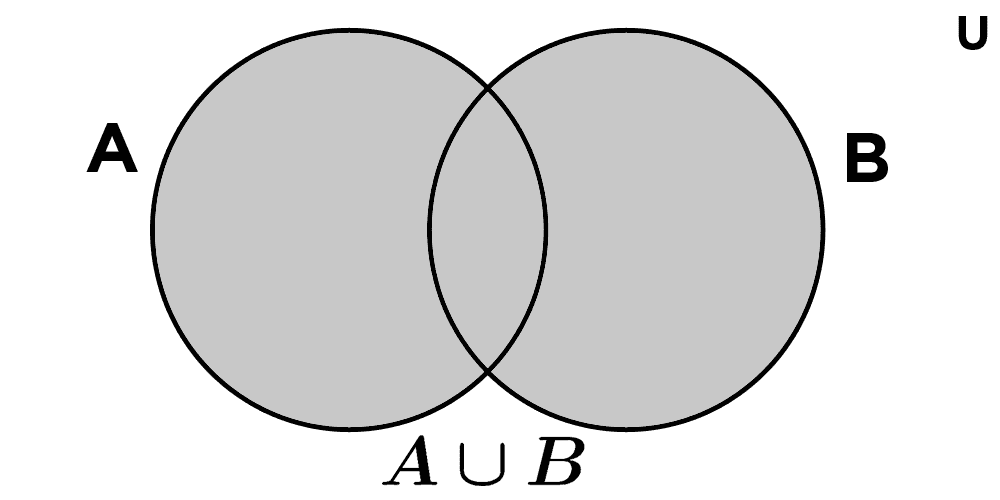
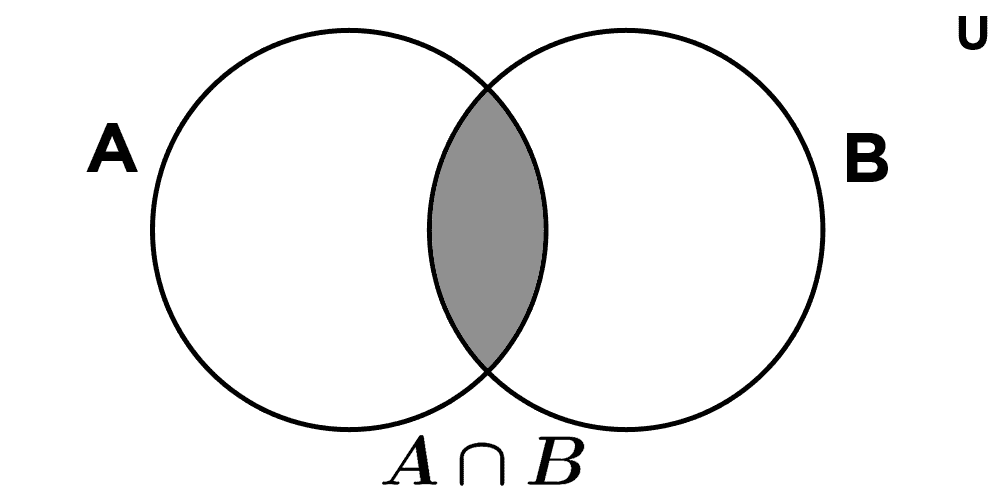
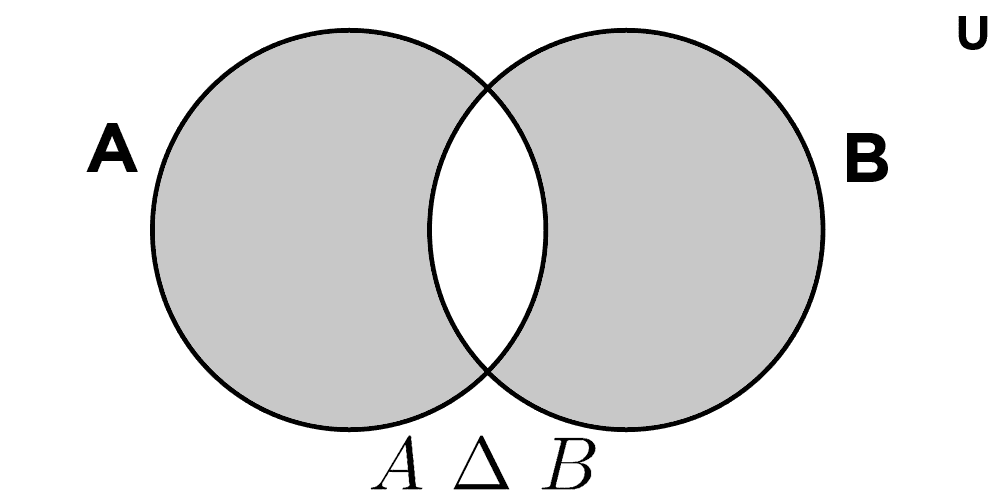

Otros artículos que pueden interesarte