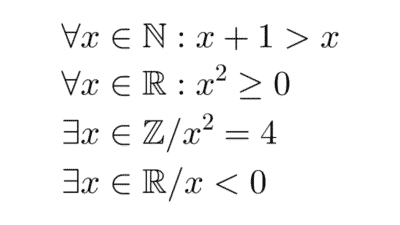
Proposiciones lógicas: qué son, ejemplos y tipos
Las proposiciones lógicas son enunciados que pueden ser calificados como verdaderos o falsos, pero no ambos simultáneamente. Estos enunciados son el elemento fundamental de la lógica y deben ser claros y precisos, sin ambigüedades, para que su valor de verdad pueda ser determinado objetivamente.
Por ejemplo, “la Tierra es un planeta” es una proposición cuyo valor de verdad es verdadero, mientras que “2 + 2 = 5” es una proposición falsa. Sin embargo, no todos los enunciados son proposiciones; frases como “¿qué hora es?” o “¡estudia más!” no pueden ser verdaderas ni falsas, por tanto, no son proposiciones.
Índice
Ejemplos
Otros ejemplos de proposiciones son:
- “Júpiter es el planeta más grande del Sistema Solar”.
- “La Tierra órbita alrededor del Sol”.
- “2 es un número par”.
- “El Támesis es caudaloso”.
- “El café contiene cafeína”.
- “El piano es un instrumento musical”.
Ejemplos de oraciones que NO son proposiciones:
- “¡Cierra la puerta!”.
- “¡Qué hermoso día!”.
- “¿Cuánto cuesta este producto?”.
- “Gire hacia la izquierda”.
- “Ojalá llueva mañana”.
Del mismo modo, las oraciones sin sentido o las que contienen variables indefinidas (como “x es mayor que 3”, sin saber qué es x) no son proposiciones hasta que se especifica el valor de la variable.
Tipos de proposiciones
Existen dos clases de proposiciones, ellas son:
- Proposiciones simples o atómicas: son aquellas que no pueden descomponerse en partes más pequeñas sin perder su significado, expresan una única idea y no contienen conectivos lógicos. Por ejemplo, “la Tierra gira alrededor del Sol” es una proposición simple.
- Proposiciones compuestas o moleculares: son aquellas formadas a partir de proposiciones simples utilizando conectores lógicos, como “hoy es lunes y hace frío”, donde el conector “y” (conjunción) une dos afirmaciones. Otros conectivos comunes incluyen "o" (disyunción), "si... entonces..." (condicional) y "no" (negación), “si y sólo si” (bicondicional).
Ejemplos de proposiciones simples son los vistos anteriormente, mientras que algunos ejemplos de proposiciones compuestas son:
- "No está lloviendo". El operador "no" (negación) modifica la frase "está lloviendo".
- "Hace sol y hace calor". Aquí el conector "y" (conjunción) une las frases "hace sol" y "hace calor".
- "Voy al cine o me quedo en casa". El conector "o" (disyunción) une las frases "voy al cine" y "me quedo en casa".
- "Si estudias, entonces aprobarás". El conectivo "si... entonces" (condicional) une las frases "estudias" y "aprobarás".
- "Un número es par si y sólo si es divisible entre 2". El conector lógico "si y sólo si" (bicondicional) une las frases "un número es par" y "es divisible entre 2".
Algunos ejemplos más complejos donde se involucra más de un conector:
- "No es cierto que Juan venga a la fiesta y María no venga". Aquí, el conector "no" niega la conjunción "Juan viene a la fiesta y María no viene".
- "Si hace frío y está nublado, entonces llevaré abrigo o me quedaré en casa". En esta proposición, el conector "si... entonces" (condicional) une "hace frío y está nublado" (donde el "y" une "hace frío" y "está nublado").
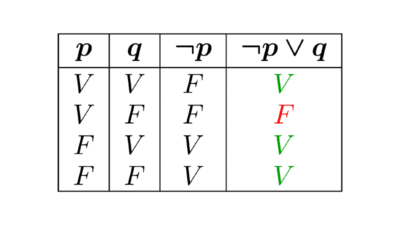
La veracidad o falsedad de una proposición compuesta depende del valor de verdad de las proposiciones simples que la componen y de la manera en que están combinadas. En función de si estas son verdaderas o falsas, la proposición compuesta tendrá un valor u otro. Por ejemplo, la proposición “Marte y Venus son planetas” es verdadera si son ciertas las proposiciones “Marte es un planeta” y “Venus es un planeta”, en este caso, es así. Este análisis se realiza utilizando tablas de la verdad.
Simbología
En lógica, para denotar a las proposiciones se utilizan las últimas letras del alfabeto en minúscula (p, q, r, s, …), a estas letras se las llama variables proposicionales. El valor verdadero se indica con la letra “V”, el número 1 o la letra “T” (de true, ‘verdadero’ en inglés); mientras que el valor falso se indica con la letra “F” o el número 0.
Cada conector lógico tiene su símbolo específico, estos pueden verse en la siguiente tabla.
| Conectivo | Símbolo |
|---|---|
| Negación | ¬ |
| Conjunción | ∧ |
| Disyunción | ∨ |
| Condicional | → |
| Bicondicional | ↔ |
Por ejemplo, dadas las siguientes proposiciones:
- p: "Está lloviendo".
- q: "Llevaré paraguas".
Se pueden formar, entre otras, estas nuevas proposiciones:
- ¬p: “No está lloviendo”.
- ¬q: “No llevaré paraguas”.
- p ∧ q: "Está lloviendo y llevaré paraguas".
- p ∨ q: "Está lloviendo o llevaré paraguas"
- p → q: "Si está lloviendo, entonces llevaré paraguas"
- p ↔ q: "Está lloviendo si y sólo si llevaré paraguas"
Bibliografía
- Acevedo González, G. (2011). Lógica Matemática. Universidad Nacional Abierta y a Distancia (UNAD).
- Garrido, M. (1974). Lógica simbólica (4ta edición). Tecnos.
- Puyau, H. y Roetti, J. (1976). Elementos de Lógica Matemática. Editorial Universitaria de Buenos Aires.
- Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.
Deja una respuesta

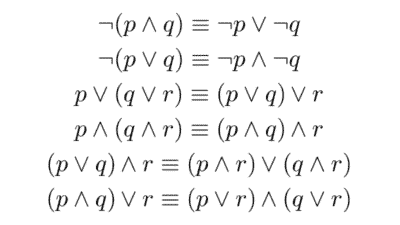


Otros artículos que pueden interesarte