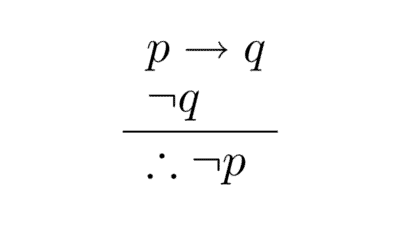
Lógica matemática
La lógica matemática o lógica simbólica es una rama de las matemáticas que estudia los principios del razonamiento válido y las estructuras formales que lo sustentan. Analiza proposiciones, inferencias y pruebas mediante símbolos y reglas precisas, con el fin de representar y manipular argumentos de forma rigurosa.
El objetivo de la lógica matemática es identificar qué conclusiones se derivan necesariamente de ciertos supuestos, sin depender del contenido específico de las proposiciones. Para lograrlo, traduce los razonamientos a un lenguaje simbólico que permite evaluar su validez solo por su forma. Este proceso, llamado formalización, es fundamental para distinguir los argumentos sólidos de las falacias que solo lo parecen.
La lógica matemática es clave no solo en la investigación matemática, sino también en campos tan diversos como la informática, la filosofía y el derecho. En computación y programación, proporciona las bases para diseñar algoritmos. En filosofía, ayuda a analizar y clarificar argumentos complejos. Además, la lógica se aplica en la vida cotidiana para estructurar razonamientos claros y evitar contradicciones, mientras que en el derecho permite formalizar normas y evaluar la coherencia de leyes y argumentos legales.
Índice
Tipos de lógica
La lógica matemática se divide en varias subramas, cada una enfocada en distintos aspectos del razonamiento formal. Estas son las más importantes:
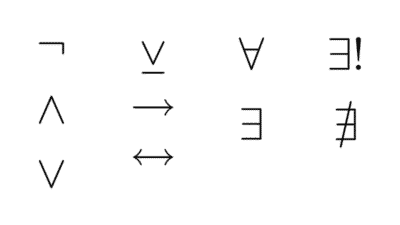
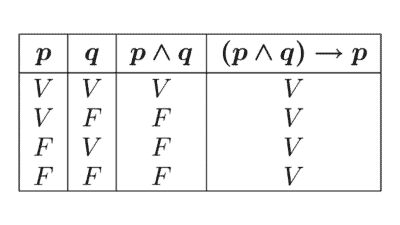
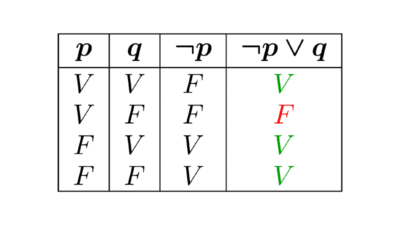
- Lógica proposicional: estudia las proposiciones consideradas como unidades indivisibles y cómo se relacionan mediante conectores lógicos como “y”, “o”, “no”, “si… entonces”, “si y sólo si”. No analiza la estructura interna de los enunciados, solo su forma lógica.
- Lógica de predicados: profundiza más allá de la lógica proposicional al introducir variables, cuantificadores y predicados, lo que permite analizar la estructura interna de las proposiciones. Es ideal para representar enunciados generales como “todos los humanos son mortales”.
- Teoría de conjuntos: es la base formal sobre la que se construyen gran parte de las matemáticas modernas. Estudia los conjuntos (colecciones bien definidas de objetos) y las relaciones entre ellos, como pertenencia, inclusión, unión o intersección.
- Lógica modal: incorpora conceptos como necesidad, posibilidad o creencia, ampliando la lógica clásica para razonar sobre lo que puede ser o debe ser. Por ejemplo, “es posible que llueva” no afirma que llueve, sino que existe una posibilidad lógica de que ocurra.
- Teoría de la demostración: se centra en el estudio formal de las pruebas matemáticas, analizando qué puede demostrarse dentro de un sistema lógico y cómo se construyen esas demostraciones. Por ejemplo, se pregunta si es posible derivar una proposición a partir de ciertos axiomas usando solo reglas válidas de inferencia.
- Teoría de modelos: estudia la relación entre los lenguajes formales y las estructuras que los interpretan, conocidas como modelos. Por ejemplo, analiza si una teoría como la aritmética es verdadera dentro de los números naturales como modelo.
- Teoría de la computabilidad: explora los límites de lo que puede resolverse mediante algoritmos. Por ejemplo, demuestra que no existe un procedimiento general para determinar si cualquier programa se detendrá o entrará en un bucle infinito (el famoso “problema de la parada”).
Contenidos de lógica matemática
Subir

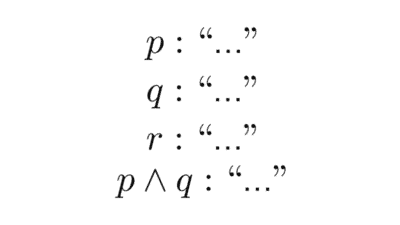
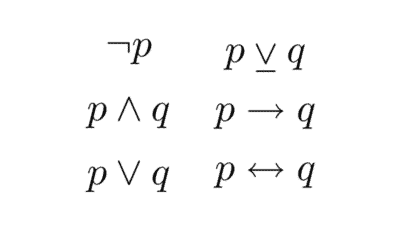


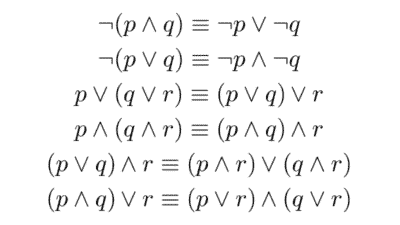
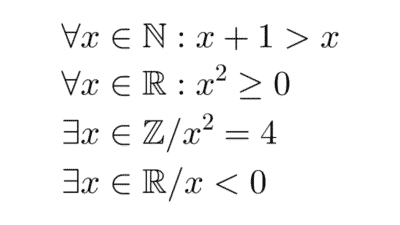

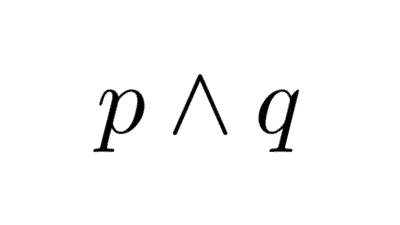
Deja una respuesta