Producto cartesiano

Ejemplos

1) Dados los conjuntos A = {1, 2} y B = {a, b}, el producto cartesiano es:

A × B = {(1, a), (1, b), (2, a), (2, b)}

2) Sean C = {x, y, z} y D = {0, 1}, su producto cartesiano es:

C × D = {(x, 0), (x, 1), (y, 0), (y, 1), (z, 0), (z, 1)}

3) El producto cartesiano de los conjuntos A = {a, b, c} y B = {1, 2} es el conjunto:

A × B = {(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)}

4) Dado el conjunto ℕ (números naturales) y el conjunto B = {0, 1}, el producto cartesiano entre ambos tendrá infinitos elementos, expresado por comprensión es:

N × B = {(n, b) | n ∈ N, b ∈ {0, 1} }

Algunos de los pares ordenados de este conjunto son (1, 0), (2, 0), (1, 1), (5, 0), etc.

5) El conjunto de los números racionales se define como el producto cartesiano entre el conjunto de los números enteros y él mismo pero sin el cero:

Q = Z × Z*

6) El conjunto de los números complejos se define como el producto cartesiano entre el conjunto de los números reales y él mismo:

C = R × R

El producto cartesiano de un conjunto consigo mismo es:

A × A = A² = {(a, b) | a ∈ A ∧ b ∈ A}

Por ejemplo, con A = {1, 2}, se tiene A × A = A² = {(1, 1), (1, 2), (2, 1), (2, 2)}.

Producto cartesiano de tres conjuntos

Ejemplo: dados los conjuntos A = {1, 2}, B = {x} y C = {a, b}, se tiene:

A × B × C = {(1, x, a), (1, x, b), (2, x, a), (2, x, b)}

Cómo calcular el producto cartesiano

Veamos algunas técnicas que podemos utilizar para facilitar el cálculo de los productos cartesianos. Esto solo servirá cuando tengamos conjuntos de pocos elementos y debamos expresar el producto por extensión. En el caso de tratar con conjuntos infinitos, dejar expresado el producto cartesiano como en la definición, es decir, por comprensión, es más que suficiente.

Producto cartesiano de 2 conjuntos

Al tratar con pares ordenados, podemos utilizar un plano con coordenadas cartesianas para representar los elementos de ambos conjuntos y hallar su producto. En el eje horizontal situamos los elementos del primer conjunto y en el eje vertical los del segundo conjunto. Luego, formamos los pares ordenados correspondientes.

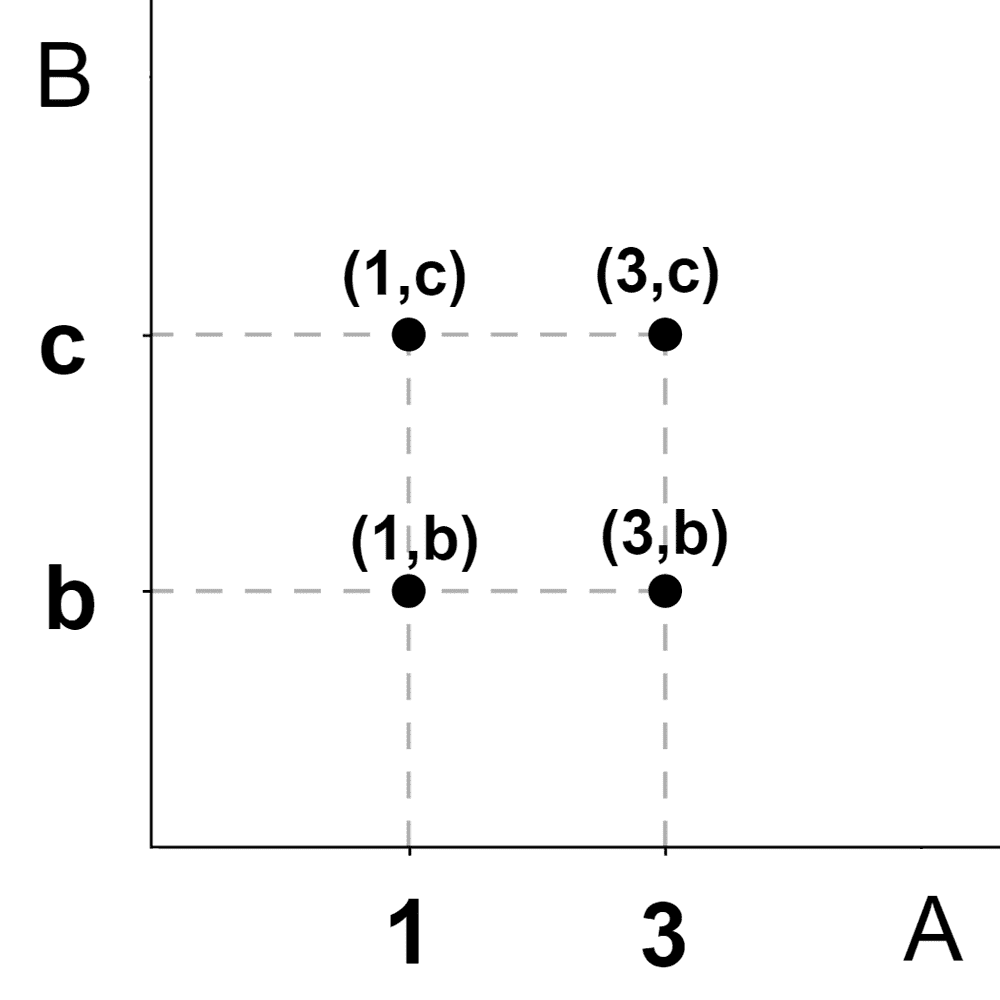
Por ejemplo, sean los conjuntos A = {1, 3} y B = {b, c}, buscamos calcular A×B. El gráfico cartesiano nos quedaría de la siguiente manera:

De aquí extraemos que A×B = {(1,b), (1,c), (3,b), (3,c)}. Otra forma más compacta consiste en una tabla que sigue la misma lógica que el gráfico, como la siguiente:

c	(1, c)	(3, c)
b	(1, b)	(3, b)
A × B	1	3

De aquí llegamos a los mismos pares ordenados para el producto cartesiano.

Producto cartesiano de 3 conjuntos

En el caso de tener tres conjuntos, la representación de A×B×C no sería en un plano, sino en el espacio, debido a las tres componentes de la terna. Sin embargo, para no complicarnos haciendo gráficos tridimensionales, podemos primero calcular el producto de los dos primeros conjuntos y, utilizando los pares obtenidos, formar las ternas con el proceso anterior. Es decir, hacer (A × B) × C.

Ejemplo: sean A = {a, b, c}, B = {1, 2} y C = {7, 8}. Calculamos primero A×B:

2	(a, 2)	(b, 2)	(c, 2)
1	(a, 1)	(b, 1)	(c, 1)
A × B	a	b	c

Entonces, A × B= {(a, 2), (b, 2), (c, 2), (a, 1), (b, 1), (c, 1)}. Estos pares obtenidos los situamos ahora en el eje horizontal y en el vertical colocamos los elementos de C:

8	(a, 2, 8)	(b, 2, 8)	(c, 2, 8)	(a, 1, 8)	(b, 1, 8)	(c, 1, 8)
7	(a, 2, 7)	(b, 2, 7)	(c, 2, 7)	(a, 1, 7)	(b, 1, 7)	(c, 1, 7)
A × B × C	(a, 2)	(b, 2)	(c, 2)	(a, 1)	(b, 1)	(c, 1)

De aquí ya podemos extraer todas las ternas de A × B × C = {(a, 2, 8), (b, 2, 8), (c, 2, 8), (a, 1, 8), (b, 1, 8), (c, 1, 8), (a, 2, 7), (b, 2, 7), (c, 2, 7), (a, 1, 7), (b, 1, 7), (c, 1, 7)}

Propiedades del producto cartesiano

La operación de producto cartesiano cumple con determinadas propiedades relacionadas con las operaciones entre conjuntos, algunas de ellas son:

Propiedad	Simbología
Distributividad respecto a la unión, intersección y diferencia de conjuntos	(A ∪ B) × C = (A × C) ∪ (B × C) (A ∩ B) × C = (A × C) ∩ (B × C) (A - B) × C = (A × C) - (B × C)
Complemento del producto cartesiano	(A × B)c = (Ac × Bc) ∪ (Ac × B) ∪ (A × Bc)
El producto cartesiano de dos conjuntos es vacío si alguno de los dos es vacío.	A × B = ϕ ↔ A = ϕ ∨ B=ϕ
Dos conjuntos A' y B' están incluidos en A y B respectivamente si y solo sí su producto cartesiano está incluido en el producto cartesiano de A y B.	A' ⊆ A ∧ B' ⊆ B ↔ A' × B' ⊆ A × B

Bibliografía

• Grimaldi, R. (1997). Matemáticas discreta y combinatoria (3ra edición). Addison-Wesley Iberoamericana.
• Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.
• Vidal, J. (2010). Teoría de conjuntos. Universidad de Valencia.
• Zill, D. y Dewar, J. (2012). Álgebra, trigonometría y geometría analítica (3ra edición). McGraw Hill.